VI. Adatszerkezetek: gráfok

Elsõ nekifutás: gráfok fajtái, tárolásuk

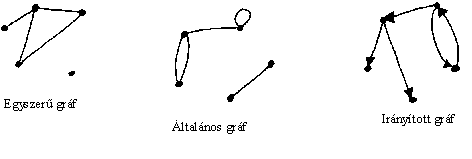
Az alkalmazott matematikában a gráfok kiemelten hasznos adatszerkezetek. A célnak megfelelõen többfajta gráfot használunk, éspedig:

Az egyszerû gráf véges ponthalmaz, melyben két különbözõ pont (más néven csúcs) vagy össze van kötve (tartozik hozzájuk él), vagy nincs. Egy pont nem lehet összekötve saját magával, és kétszeresen összekötött pontok sincsenek. Alakalmazására példa egy elektromos hálózat, melyben városok vannak villanyvezetékkel összekötve, vagy egy úthálózat, ahol az a kérdés, hogy honnan lehet eljutni hová. Hacsak a szövegbõl másképpen nem következik, mindig egyszerû gráfokról beszélünk.

Az általános gráfban két pont többszörösen is össze lehet kötve, illetve a hurokél (egy pontból saját magába vezetõ él) is megengedett.

Az irányított gráfban az éleknek iránya is van (tehát külön élnek számít az A-ból B-be és a B-bõl A-ba mutató él). Példa rá egy keresztezõdés-rendszer egyirányú utcákkal (a kétirányú utcát egy oda- és egy visszafelé mutató él jelentheti), vagy személyek közti szimpátiát ábrázoló gráf (a szimpátia nem feltétlenül kölcsönös). Az irányított gráfban általában megengedettek a többszörös, és olykor a hurokélek.

Ezen kívül az élekhez lehet számot is rendelni (súlyozott gráf), ilyen pl. egy csatornarendszer, ahol megadjuk az egyes csatornák áteresztõ képességét.

Egyszerû gráfok tárolására kétféle módszer is létezik. A csúcsmátrix NxN-es tömb (G[1..N,1..N], ahol N a pontok száma). G[i,j]=1, ha az i. és j. pont össze van kötve, különben 0. Ezenkívül G[i,i]=0 (nincs hurokél) és G[i,j]=G[j,i] (a mátrix szimmetrikus). Ha a gráfot így ábrázoljuk, könnyen választ kaphatunk az egyszerû gráfoknál feltehetõ egyetlen kérdésre: össze van-e kötve két adott pont? Ha azonban az élek száma kicsi a csúcsokéhoz képest, vagyis a mátrixban nagyon sok a 0 (hézagos mátrix), ez az ábrázolási forma helypazarló.

Az élmátrix a gráfok éleit tárolja, például egy G[1..E] tömbben, ahol E az élek száma. G elemei számpárok, pl. G[a]=(i,j), vagyis az a. él az i. és j. csúcsot köti össze. Itt nehezebb megállapítani két pont összekötöttségét, viszont könnyebb pl. az összes élt felsorolni.

1. feladat: írj programot, mely beolvassa N-t, majd beolvas egy NxN-es, 0-kból és 1-ekbõl álló mátrixot, és eldönti, hogy ez lehet-e egyszerû gráf csúcsmátrixa!

2. feladat: írj programot, mely beolvassa N-t, E-t, majd E darab számpárt (egyszerû gráf élmátrixa). A program az ezután beírt számpárokra eldönti, hogy össze van-e kötve az adott két pont!

3. feladat: írj programot, mely megadott N és csúcsmátrix esetén kiírja az egyszerû gráf éleit (minden élt csak egyszer)!

4. feladat: módosítsd a 2. feladat programját úgy, hogy az élmátrix beadása után a program állítsa elõ a gráf csúcsmátrixát!

Akárhogyan is ábrázoljuk az egyszerû gráfokat, ha a programban meg tudjuk valósítani a Vanél(i,j) függvényt (i. és j. csúcs össze van-e kötve), minden információ rendelkezésünkre áll a gráfról.

Az egyszerû gráfok mintájára ábrázoljunk egyéb gráfokat. Általános gráf élmátrixos ábrázolása egyszerû: a többszörös éleket többször fel kell sorolni, és megengedett az (i,i) típusú él is. Csúcsmátrixban ha G[i,j]>1, az annyiszoros élt jelenthet.

Irányított gráf élmátrixában különbséget teszünk (i,j) és (j,i) él között (elõbbi jelentse az i. pontból a j. pontba mutató élt). Hasonlóképpen a csúcsmátrixnak nem kell szimmetrikusnak lenni, éspedig G[i,j]=1 jelentse azt, hogy az i. pontból mutat él a j. pontba.

Súlyozott egyszerû gráf csúcsmátrixában G[i,j] lehet az (i,j) él súlya (0, ha nincs él). Általános súlyozott gráfokat nem lehet egyszerû csúcsmátrixszal ábrázolni. Súlyozott gráf élmátrixában az éleket (i,j,s) számhármasok ábrázolják: i. pontból j. pontba mutató él, s súllyal.

Második nekifutás: gráfok jellemzése, alapvetõ gráf-algoritmusok

Sétának nevezzük gráfban az (a b)(b c)(c d)... egymáshoz csatlakozó élek sorozatát. Vonal, ha minden él csak egyszer szerepel benne. Út az a vonal, mely minden ponton csak egyszer megy át. Kör az a vonal, melyben az elsõ él kezdõpontja és az utolsó él végpontja megegyezik, és minden más ponton csak egyszer megy át. Ezeknek az elnevezéseknek nincsen túl nagy jelentõsége, más könyvekben mást jelentenek. A feladatból általában kiderül, hogy mirõl van szó.

Ha például két pont között van séta, akkor biztos, hogy út is van. Általában utakat keresünk, mert azok száma véges, és általában rövid úton szeretnénk egyik pontból a másikba jutni. Ha egyik pontból a másikba két út is vezet, akkor a gráfban biztosan van kör (az irányított gráfokat kivéve). Vonalról van szó, ha egy gráfot a ceruza felemelése nélkül, minden élt csak egyszer érintve akarunk megrajzolni.

Gráfban egy pont foka a pontban összefutó élek száma. Hurokél kettõnek számít! Irányított gráfnál beszélhetünk külön kimenõ és befutó fokszámról.

Gráf összefüggõ, ha bármely két pontja között van út (elég azt megállapítani, hogy egy kiválasztott pontból az összes többihez van-e út). Egy gráf diszjunkt részgráfjainak pontjai között nincsen út.

1. feladat: a következõ egyszerû gráf élmátrixa alapján állapítsd meg, hogy összefüggõ-e! (Próbáld meg lerajzolni.) Ha nem összefüggõ, hány diszjunkt része van? Hány kör van benne?
(1 2) (1 8) (2 9) (2 10) (3 4) (3 11) (4 11) (5 6) (5 11) (7 8) (7 9) (7 10)

A legfontosabb gráfos algoritmus út keresése két pont között. Erre két algoritmus is kínálkozik. Mindkét esetben A és B pont között keresünk utat egyszerû gráfban (ebbõl a szempontból az általános gráfok többszörös élei és hurokélei lényegtelenek, irányított gráfokra pedig lényegi változtatás nélkül mûködnek a módszerek). Az algoritmusok felsorolják a gráf A-ból elérhetõ összes pontját (gráfbejárás), tehát megtalálják az A-t tartalmazó maximális összefüggõ részgráfot. Ha B közöttük van, van út.

A szélességi keresésnél vesszük A pont összes szomszédját, majd ezeknek a pontoknak az összes szomszédját, és így tovább. Ha egy pont egyszer már sorra került, azt többször nem soroljuk fel. Így végül felsoroljuk az összes olyan pontot, mely A-ból elérhetõ. Ha B köztük van, van út a két pont között. Magát az utat is megkaphatjuk, ha pl. minden sorra kerülõ csúcshoz feljegyezzük, hogy melyik csúcsból jutottunk oda. Így B-bõl visszafelé lépegetve eljutunk A-ig.

Ennek rajzos megoldása: írjunk A ponthoz 0-t. Írjunk A összes szomszédjához 1-et. Írjunk ezek még nem beszámozott szomszédaihoz 2-t stb... Így végül beszámozzuk mindazokat a pontokat, melyek A-val közös összefüggõ részgráfban vannak. Ráadásul minden pontnál az a szám szerepel, hogy A-ból legrövidebben hány lépésben érhetõ el. B pontból a számok csökkenõ sorrendjében visszafelé lépegetve eljuthatunk A-ig, így megkaptuk a legrövidebb A-B utat.

A következõ algoritmus sort használ a felsorolás alatt lévõ pontok tárolására (kiveszünk egy pontot a sor végérõl, a sor elejére pedig berakjuk a fel nem sorolt szomszédait - vigyázz, itt a sor vége kerül sorra, és az eleje vár a legtöbbet!). V tömb a már felsorolt pontokról tárolja, hogy honnan jutottunk el odáig.

V[1..N]:=0, Sorba(A)
V[A]:= -1 {mindegy, csak ne 0 legyen}
Ciklus amíg a sor nem üres
   Sorból(X)
   Ciklus I:=1..N
      Ha van él X és I között és V[I]=0 akkor Sorba(I), V[I]:=X
   Ciklus vége
Ciklus vége

V tömbben tehát 0 lesz azoknál az elemeknél, melyek A-ból nem érhetõk el, egyébként pedig annak a csúcsnak a száma, melybõl az illetõ pontba az A-ból induló legrövidebb úton eljuthatunk.

2. feladat: módosítsd a szélességi keresés algoritmusát arra az esetre, amikor csak A-ból B-be vezetõ utat keresünk (a ciklus akkor is leáll, ha B már sorra került).

3. feladat: írj programot, mely élmátrixszal megadott gráfról eldönti, hogy összefüggõ-e! (Nem kell mást tenni, mint tetszõleges pontból alkalmazni a szélességi bejárást, és megnézni, hogy V elemei között van-e 0.)

4. feladat: írj programot, mely kiírja élmátrixszal megadott gráf két adott pontja közötti legrövidebb utat (ha van).

A Backtrack bemutatásánál található lóugrás-probléma is megfogalmazható gráfbejárással: a pontok a sakktábla mezõi, két pont között van él, ha az egyik mezõ a másikból lóugrással elérhetõ. Így könnyen elkészíthetõ a gráf csúcsmátrixa. Ennek alapján viszont szélességi kereséssel nagyon könnyû megadni a legrövidebb utat két pont között.

5. feladat: írd meg a lóugrás-programot egyszerûbben, szélességi kereséssel! A csúcsmátrixot nem is szükséges elkészítened, hiszen a Szam2koord és Lo függvényekkel meg tudod adni, van-e él két mezõ között.

A másik gráfbejáró algoritmus a mélységi keresés. Elve: elindulunk A pontból, vesszük egy még fel nem sorolt szomszédját, annak a szomszédját, stb. Ha már nem tudunk tovább lépni (a vizsgált csúcsból nincs él még fel nem sorolt csúcshoz), visszalépünk az elõzõ csúcsra. Ez Backtrack-jellegû probléma, sõt, verem segítségével is meg oldható: a verem mindig tárolja, hogy a vizsgált X pontba honnan érkeztünk. V tömbben most 1-gyel jelöljük a már felsorolt pontokat.

V[1..N]:=0, X:=A, V[X]:=1, Verembe(0)
Ciklus amíg a verem nem üres
   I:=1
   Ciklus amíg I<=N és (nincs (X,I) él vagy V[I]=1) {X-nek új szomszédot keresünk}
      I:=I+1
   Ciklus vége
   Ha I<=N   akkor Verembe(X), V[I]:=1, X:=I {ha van új szomszéd}
          különben Verembõl(X) {visszalépés az elõzõre}
Ciklus vége

Az algoritmus úgy ér véget, hogy felsoroltuk az összes elérhetõ pontot, és több él nem lévén, visszaléptünk A ponthoz. A verembe azért tettünk be 0-t az elején, mert végül, mivel A-hoz már nem találunk új szomszédot, az algoritmus megpróbál A megelõzõjére visszalépni, és ez hibát okozna.

A veremben minden lépésben az A-tól a vizsgált pont megelõzõjéig tartó út állomásai vannak. Ha B pontba érkezéskor leállítjuk a ciklust, a veremben éppen az A-B út lesz.

6. feladat: írj programot, mely élmátrixszal megadott gráfban két pont között utat keres mélységi kereséssel!

Mélységi kereséssel nem a legrövidebb utat találjuk meg. De mi a helyzet akkor, ha a gráf élei nem egyenlõ hosszúak (súlyozott gráf)? A szélességi keresés által talált út a legkevesebb élbõl áll, de nem biztos, hogy a legrövidebb (illetve, ha súlyról beszélünk, a legkönnyebb). Hasonlóképpen a legrövidebb lóugrás-sorozat kereséséhez (V. fejezet), ismét a backtrack egy változatát használjuk. A lényeg az, hogy a gráf egy pontját ismét kiválaszthatjuk, ha rövidebb úton jutunk oda A-ból, mint korábban.

Most V tömbben nem azt tároljuk, hogy voltunk-e már az adott pontban, hanem, hogy A-ból milyen hosszú úton juthatunk oda (a hosszt a program menet közben számolja, elõrelépésnél a megfelelõ él súlyával növeli, visszalépésnél csökkenti). V elemeinek kezdõértéke: kellõképpen nagy szám (az algoritmus szempontjából +végtelen, gyakorlatban az elõforduló úthosszaknál nagyobb szám). Amikor új szomszédot keresünk, olyan szomszédok jöhetnek szóba, amelyekbe az eddiginél rövidebb úton jutunk.

7. feladat: írj programot, mely beolvassa súlyozott egyszerû gráf élmátrixát (most az éleknél a két csúcson kívül a súlyt is meg kell adnunk), majd adott A és B csúcsok között megkeresi a legkönnyebb utat!

8. feladat: írj programot, mely élmátrixszal megadott egyszerû gráfban megszámolja a diszjunkt részgráfokat! Tipp: tetszõleges pontból kiindulva valamelyik kereséssel bejárjuk a gráfot, így kapunk egy összefüggõ, többitõl diszjunkt részt. A maradék pontokra ezt ismételjük, amíg csak el nem fogynak a pontok.