VII. Adatszerkezetek: fák

Elsõ nekifutás: a fák tulajdonságai

Fának nevezzük az összefüggõ, körmentes egyszerû gráfokat. Érdemes felsorolnunk a fák néhány jellegzetes tulajdonságát.

Fában két pont között pontosan egy út létezik. Létezik, mert a gráf összefüggõ, és pontosan egy, mert ha kettõ lenne, kör is lenne.

Ha fához hozzáteszünk egy élt, már nem lehet fa. (i j) él hozzávételével ugyanis kört kapnánk, hiszen eddig is volt a két csúcs között út, és most lett még egy, tehát kör keletkezett.

Fából egy élt elhagyva már nem lehet fa. Ha ugyanis fa lenne, akkor abba az iménti élt visszatéve megint csak fát kapnánk (az eredetit), ami az elõzõ bekezdés szerint nem lehet.

Úgy is fogalmazhatnánk, hogy a fa a lehetõ legkevesebb élt tartalmazza, ami szükséges az összefüggõséghez.

Ha egy fában E él és P csúcs van, akkor P=E+1. Bizonyítás: vegyünk egy fát. Ebben biztosan van olyan pont, melynek foka 1. Ha ugyanis minden pont foka legalább 2 lenne, akkor el tudnánk indulni egy pontból, és ha a pont még nem került sorra, tovább tudnánk lépni egy másik, még fel nem használt élen. Mivel véges számú pont van, elõbb-utóbb olyan pontot érintünk, ami már volt. Ekkor viszont találtunk egy kört, ami ellentmondás. Miután van 1-fokú pont, vágjuk le a fáról az élével együtt. Ezzel nem keletkezett kör, és az összefüggõség sem sérült. A maradék-fát ismét megnyessük, egészen addig, míg egy pont (és nulla él) marad. Mivel a nyesegetés során ugyanannyi pontot vettünk el, mint élt, az eredeti fában is eggyel több pont volt, mint él.

Ha egy összefüggõ gráfban P=E+1, akkor az fa. Ha ugyanis nem lenne fa, elhagyhatnánk belõle éleket, hogy az legyen (nyilván körök voltak benne, azért nem volt fa). Az így kapott fában viszont P=E+1, pedig most kevesebb él van benne, mint eredetileg. Ez ellentmondás.

Mire jó ez? A körmentesség közvetlenül elég nehezen mutatható ki egy gráfról. Az összefüggõség egyszerû (ld. VI. fejezet). Ha viszont van egy összefüggõ gráfunk, csak meg kell számolni a pontjait és éleit, hogy eldönthessük, körmentes-e (vagyis fa).

Egy összefüggõ gráf feszítõfája az a fa, amely a gráf minden pontját, és éleinek egy részét tartalmazza. Feszítõfát többféleképpen kaphatunk (a következõ algoritmusokat bizonyítás nélkül közöljük. A bizonyítással meg lehet próbálkozni. A megértéshez célszerû rajzolni!):

1. Vegyük ki a gráf összes élét. Tegyük vissza sorban azokat az éleket, melyek még nem alkotnak kört a már bent lévõkkel. Ezt P-1-szer kell megcsinálni. (Hogyan állapítható meg, hogy (i,j) él visszatevése nem alkot kört? Ha már létezik út az i. és j. csúcs között, akkor az él hozzávétele kört ad, különben nem.) (Kruskal algoritmusa)

2. Induljunk ki egy pontból. Keressünk egy olyan élt és pontot, mely az eredeti gráfban ehhez kapcsolódott. Aztán az így kapott fához kapcsoljunk hozzá újabb pontot (a hozzákapcsolt pontok kezdetben 1-fokúak lesznek). Ezt P-1-szer kell ismételni. (Prim algoritmusa)

3. Keressünk a gráfban egy kört, és hagyjuk el egy élét. Ezt ismételjük mindaddig, míg P-1 élünk nem marad.

A 3. algoritmus nehezen megvalósítható, mert a gráfban nem egyszerû kört keresni. A Kruskal-féle algoritmus legegyszerûbb megvalósítása, ha a csúcsokat megszámozzuk. Az algoritmus voltaképpen diszjunkt fákat kötöget össze. Ha egy éllel két fát összekötünk, kapja a két fa összes pontja ugyanazt a kódszámot (valamelyik pontjuk kódszámát). Így könnyû eldönteni, hogy a kérdéses él eddig még diszjunkt fákat köt-e össze (ez esetben betehetõ). Prim algoritmusa esetén a helyzet még egyszerûbb: vannak pontok, melyek már bekerültek a fába, és vannak, amelyek még nem.

1. feladat: írj programot, amely élmátrixszal megadott összefüggõ gráfhoz feszítõfát keres Prim algoritmusa segítségével!

Bonyolítja a helyzetet, ha a gráf élei súlyozottak. Ekkor a feladat a legolcsóbb/legkönnyebb feszítõfa megkeresése (élei súlyának összege minimális). Ez gyakorlati alkalmazás szempontjából is fontos: ha városok közötti elektromos hálózatot akarnak kiépíteni (ez fa lesz, újabb vezetékek már fölöslegesek), nem mindegy, mennyi vezetéket használnak.

Az elõzõ algoritmusok módosítása: az 1. és 2. algoritmusban az új él kiválasztásakor az összes szóba jövõ él közül (tehát amelyeket még nem tettünk be, és diszjunkt fákat, illetve fát és pontot kötnek össze) a legkisebb súlyút kell kiválasztani. A 3. algoritmusnál pedig a szóba jövõ élek közül mindig a legnehezebbet kell elhagyni.

2. feladat: írj programot, amely élmátrixszal megadott súlyozott gráfban legkönnyebb feszítõfát keres!

Megjegyezzük, hogy a mélységi keresés algoritmusa (VI.fejezet) éppen egy feszítõfa mentén haladva sorolja fel a pontokat.

Miért is nevezik a fát fának? Válasszunk ki egy tetszõleges pontot, és nevezzük el a fa gyökerének. A gyökérbõl minden pont egyetlen úton érhetõ el. Az egy lépésben elérhetõket rajzoljuk a gyökér alá. A következõ szintre az ezekbõl egy, a gyökérbõl két lépésben elérhetõk kerülnek, és így tovább. Irányítsuk az éleket: egy pontból az alatta lévõ szomszédok felé mutasson a nyíl. A gyökér kiválasztásával így a fához tartozik egy irányítás is. (Az éleket ezután nem is szükséges irányítani, elég megadni a gyökeret.) Egy pontból több felé is mutathat nyíl lefelé (ezeket a szomszédokat közvetlen leszármazottaknak nevezzük), egy pontba viszont csak egyetlen pontból mutathat nyíl (ez a pont az elõzõ õse). Egyedül a gyökérbe nem mutat nyíl. Azok a csúcsok, melyeknek nincsenek leszármazottaik, a fa leveleinek nevezzük. A továbbiakban ilyen módon irányított fákról lesz szó.

Ez a szerkezet alkalmas hierarchiák (alá-fölérendeltségi viszonyok) ábrázolására, pl. egy vállalat struktúrájában a közvetlen beosztottak rendszere, a DOS könyvtár-szerkezete stb.

Megjegyzés: a fa irányításával egyszerûbb a P=E+1 tétel bizonyítása. Minden pontba egy él mutat, ráadásul minden pontba másik, kivéve a gyökeret, amibe nem mutat él. Így a gyökér kivételével a pontok összepárosíthatók az élekkel.

Második nekifutás: bináris fák

A bináris fák olyan fák, melyeknél egy pontnak legfeljebb két közvetlen leszármazottja lehet. Ha a két leszármazott sorrendje nem tetszõleges, beszélhetünk bal- és jobboldali leszármazottról. Gyakorlati megvalósításnál a fa csúcsai valamilyen adatot tartalmaznak, ezen kívül tárolnunk kell, hogy mely pontoknak melyek a közvetlen leszármazottai. Ez célszerûen N-elemû tömbben történik (N a fa pontjainak száma), ahol egy tömbelem tartalmazza az adatot, valamint a baloldali és a jobboldali leszármazott indexét. Pascal-példa:

CONST N=csúcsok száma;
TYPE Faelem:record
             elem:típus;
             bal,jobb:integer;
            end;
VAR FA:array[1..N] of Faelem;
    GY:integer; {a gyökérelem indexe}

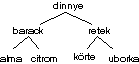
1. feladat: rajzold le a következõ tömbbel megadott fa struktúráját! (GY=1)

A bal és jobb mezõket mutatónak is hívják, mivel megmutatják, hol van a bal- és jobboldali leszármazott a tömbben. Ha egy mutató értéke 0, akkor abba az irányba nincs több leszármazott (levél bal- és jobbmutatója egyaránt 0).

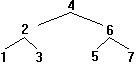
A bináris fák bejárásakor figyelembe vesszük a fa által képviselt struktúrát. Háromféle fabejárási sorrend létezik:

A bal-közép-jobb (BKJ) bejárásnál egy csúcs esetén elõször a baloldali részfáját, utána az illetõ csúcsot, utána a jobboldali részfáját dolgozzuk fel. A részfák feldolgozása rekurzívan ugyanígy történik. Példaként nézzük a következõ fát:

Az elemek felsorolása BKJ bejárással: 1, 2, 3, 4, 5, 6, 7.
Közép-bal-jobb (KBJ) bejárással: 4, 2, 1, 3, 6, 5, 7.
Végül bal-jobb-közép (BJK) bejárással: 1, 3, 2, 5, 7, 6, 4.

Rekurzív Pascal-példaprogram a BJK bejárásra (egy elem feldolgozása legyen most a kiírása). Az eljárás indítása: BJK(GY).

Procedure BJK(cs:integer);
 Begin
  if cs>0 then begin
     BJK(FA[cs].bal);
     BJK(Fa[cs].jobb);
     Write(Fa[cs].elem);
  end;
 End;

2. feladat: írd meg a BKJ és KBJ bejárás programját is, majd teszteld egy beolvasott fán!

A bináris fák jellegzetes felhasználása a rendezõfa. A rendezõfa olyan fa, melyben egy elem baloldali részfája (a baloldali leszármazott, és az abból leágazó elemek) mind nála kisebb, jobboldali részfája pedig nála nagyobb elemeket tartalmaz. A rendezõfa BKJ bejárásával az elemek sorba rendezve kerülnek feldolgozásra.

Ha egy elemet keresünk a rendezõfában, a felezéses kereséshez hasonlóan minden lépésben választunk az éppen vizsgált elem bal- és jobboldali részfája között. Ez a keresés akkor fejezõdik be a legkevesebb lépésben, ha a rendezõfa kiegyensúlyozott, vagyis az egyes elemek bal- és jobboldali részfái nagyjából ugyanannyi elemet tartal maznak. (Ellenpélda: a gyökér alma, és minden elemnek csak jobboldali leszármazottja van. A keresés ekkor a soros keresésre hasonlít.Az ilyen fákat degeneráltnak nevezzük.)

Következzék egy algoritmus E elem keresésére a bináris fában. MUT adja vissza a keresett elem indexét, vagy 0-t, ha nem létezik.

MUT:=GY
Ciklus amíg FA[MUT].elem<>E és MUT<>0
   Ha E<FA[MUT]   akkor mut:=FA[MUT].bal
               különben mut:=FA[MUT].jobb
Ciklus vége

3. feladat: írd meg a keresés algoritmusát rekurzív formában, ciklus nélkül!

A rendezõfa felépítése, vagyis a rendezés fával a beillesztéses rendezéshez (2. Pascal füzetke, A függelék) hasonló: az elemek sorban érkeznek, mindegyiknek megkeressük a helyét a fában, és beillesztjük. A fába való beillesztés részletesebb leírása:

- a keresés algoritmussal rákeresünk a beillesztendõ elemre. Ha van ilyen, nem illesztjük be (a fában minden elem csak egyszer szerepel). Ha nincs ilyen: a módosított keresõ-algoritmusnak most vissza kell adnia annak az elemnek a számát, amelybõl 0-ra futott (ez nem más, mint MUT változó elõzõ értéke).
- ezután a FA tömbben keresünk egy üres sort, betesszük az elemet, bal- és jobbmutatóját 0-ra állítjuk (minden új elem levélként kerül a fába). A rá mutató elem megfelelõ mutatóját (ami eddig 0 volt) erre az elemre állítjuk.
- Teljesen külön kell kezelni azt a speciális esetet, amikor a fa üres.

4. feladat: írd meg a fával való rendezés programját! (Az adatokat folyamatosan írjuk be, vagy egy file-ból kerülnek be. A program a beérkezõ adatoknál kiírja, hogy van már olyan a fában, vagy beilleszti a fába.)

5. feladat: hogyan keletkezhet még degenerált fa? Adj általános szabályt az elemek érkezési sorrendjére! (Véletlenszerûen érkezõ elemeknél a fa általában kiegyensúlyozott lesz.)

6. feladat: milyen módszer szerint lehet elemet törölni a rendezõfából? (Olyan elem törlése, melynek valamelyik mutatója 0, könnyû.)

Most megmutatjuk a bináris fák és bináris (kétváltozós) mûveletek kapcsolatát. Egy kétváltozós mûveletet felír hatunk infix (a mûveleti jel, vagyis operátor a két érték között van, pl. 3 + 4), prefix (+ 3 4) és postfix (3 4 +) módon is. A postfix forma elõnyeirõl ld. az I. fejezetet.

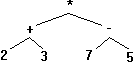A következõ fával a (2+3)*(7-5) kiszámításához szükséges mûveletvégzési sorrendet ábrázoltuk. A zárójeles kiszámítási mód a BKJ bejáráshoz kapcsolódik. Ugyanezt a fát BJK módon bejárva (2 3 + 7 5 - *) a mûvelet postfix, azaz lengyel forma (PN) szerinti jelölését kapjuk, amely verem-géppel zárójelezés nélkül is elvégezhetõ. Minden, bináris mûveleteket tartalmazó kifejezés átírható bináris fa formára, és felírható PN-ben is.

7. feladat: rajzold le bináris fával az 1/(3*((4+7)-(2+1))) mûveletet, és írd fel PN-ben is!

8. feladat: írj programot, mely egy mûveleteket ábrázoló bináris fából elõállítja a zárójeles (hagyományos, infix operátoros) kifejezést! Ha túl sok zárójelet tartalmaz, nem baj.

9. feladat: írj programot, mely kiértékel egy mûveleteket tartalmazó bináris fát! Használj rekurziót (BJK sorrendû kiértékelés).

10. feladat: írj programot, amely szabályos PN-formából elõállítja a bináris fát! Ehhez célszerû a PN formát hátulról visszafelé feldolgozni.

Harmadik nekifutás: általános fák ábrázolása

Mivel ebben az esetben egy elemnek bárhány leszármazottja lehet, a bináris fáknál használt módszer közvetlenül nem alkalmazható. Ismerkedjünk meg elõször a lista fogalmával.

A lista olyan adatszerkezet, ahol egy elemnek legfeljebb egy rákövetkezõje (leszármazottja) lehet. A lista ábrázolása a bináris fához hasonló, de egy elemhez csak egy mutató tartozik. A listában lévõ elemek logikai sorrendjét nem a táblázatban elfoglalt fizikai helyük, hanem a mutatók határozzák meg.

Az általános fák ábrázolhatók elemenként két mutatóval. Az elsõ mutató (le) az elem elsõ közvetlen leszármazottjára mutat, míg a második (mellé) az elem szülõjének következõ közvetlen leszármazottjára (vagyis az elem következõ testvérére). A mellé mutatók voltaképpen az elsõ leszármazottból kiindulva listaszerkezetben sorolják fel egy elem összes leszármazottját. Az ábrában szaggatott vonalak jelzik a fa eredeti éleit, nyilak pedig a mutatókat.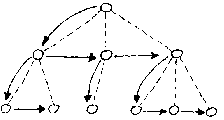

1. feladat: készíts algoritmusokat ilyen módon tárolt fa kezelésére. A legfontosabb mûveletek: elem összes közvetlen leszármazottjának kilistázása, új leszármazott felvétele (legelsõ, legutolsó, illetve tetszõleges helyre a leszármazottak listájában).

2. feladat: készíts algoritmust ilyen fák rekurzív bejárására!

3. feladat: készíts algoritmust elem törlésére összes leszármazotttjával együtt!

4. feladat: készíts interaktív fakezelõ programot! Ez a DOS könyvtárkezelõ parancsainak mintájára készíthetõ el. A program ismerje fel a CD, MD, RD, DIR és TREE parancsokat.